Pohyb loďky
Úloha číslo: 106
Z místa A plave proti proudu řeky loďka do místa B a odtud zpět do místa A. Rychlost loďky vzhledem k vodě je v obou případech stejná, a to 4 km·h−1, rychlost proudu je 1,6 km·h−1. Určete poměr doby, za kterou vykoná loďka dráhu z místa A do místa B a zpět, a doby, kterou by loďka potřebovala na vykonání této dráhy po jezeře.
Zápis
v = 4 km·h−1 rychlost loďky vzhledem k vodě r = 1,6 km·h−1 rychlost proudu t doba, za kterou loďka ujede dráhu z A do B a zpět t´ doba, za kterou loďka ujede stejnou dráhu po jezeře \(\frac{t}{t^,}\,=\,\mathrm{?}\) Nápověda 1: Rychlost loďky, která pluje z A do B
Nakreslete si obrázek pro plavbu proti proudu a vyznačte do něj rychlost loďky a rychlost proudu.
Jaká je rychlost loďky vzhledem ke břehu, pluje-li proti proudu? Bude větší nebo menší, než kdyby plula loďka po klidné vodě? O kolik? Za jaký čas urazí loďka touto rychlostí vzdálenost AB?
Nápověda 2: Rychlost loďky, která pluje z B do A
Nakreslete si obrázek pro plavbu po proudu a vyznačte do něj rychlost loďky a rychlost proudu.
Jaká bude rychlost loďky vzhledem ke břehu, pluje-li po proudu? Za jaký čas urazí loďka touto rychlostí vzdálenost BA? Jaký je celkový čas plavby?
Nápověda 3: Poměr časů
Čas, za který urazí loďka vzdálenost 2AB na klidné vodě rychlostí v, jistě snadno určíte, stejně jako hledaný poměr časů.
CELKOVÉ ŘEŠENÍ
Předpokládejme, že vzdálenost AB se rovná s km.
Obr. 1 (proti proudu):
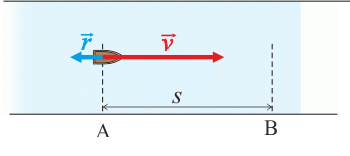
Rychlost loďky proti proudu vzhledem k břehu je daná rozdílem rychlosti loďky vzhledem k proudu a rychlosti proudu (obr. 1), tedy:
\[v_1\,=\,v-r\,.\]Obr. 2 (po proudu):
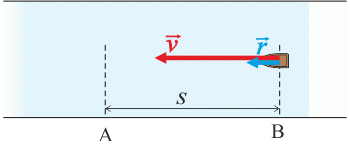
Rychlost loďky po proudu vzhledem k břehu je daná součtem obou dvou rychlostí (obr. 2):
\[v_2\,=\,v+r\,.\]Loďka urazí dráhu s proti proudu za čas:
\[t_1\,=\,\frac{s}{v_1}\,=\,\frac{s}{v-r}\,.\]Po proudu za čas:
\[t_2\,=\,\frac{s}{v_2}\,=\,\frac{s}{v+r}\,.\]Loďka se dostane z místa A do místa B a zpět za čas t:
\[t\,=\,t_1+t_2\,=\,\frac{s}{v-r}+\frac{s}{v+r}\,=\,s\,\left(\frac{1}{v-r}+\frac{1}{v+r}\right)\,=\,\frac{2v}{v^{2}-r^{2}}\,s\,.\]Na jezeře by loďka přeplula tuto vzdálenost rychlostí v za čas t´:
\[t^{,}\,=\,\frac{s}{v}+\frac{s}{v}\,=\,\frac{2}{v}s\,.\]Určíme podíl t/t´:
\[\frac{t}{t^{,}}\,=\,\frac{\frac{2v}{v^{2}-r^{2}}\,s}{\frac{2}{v}\,s}\,=\,\frac{v^{2}}{v^{2}-r^{2}}\,=\,\frac{1}{1-\frac{r^{2}}{v^{2}}}\,.\]Číselně:
\[\frac{t}{t^{,}}\,=\,\frac{4^{2}}{4^{2}-1{,}6^{2}}\,=\,\frac{16}{13{,}44}\,\dot=\,1{,}19\,.\]Odpověď
Poměr doby t, za kterou loďka urazí dráhu z místa A do místa B a zpět na řece, a doby t´, kterou by loďka potřebovala na proplutí této dráhy po jezeře, je:
\[\frac{t}{t^{,}}\,=\,\frac{\frac{2v}{v^{2}-r^{2}}\,s}{\frac{2}{v}\,s}\,=\,\frac{v^{2}}{v^{2}-r^{2}}\,=\,\frac{1}{1-\frac{r^{2}}{v^{2}}}\,.\]Číselně:
\[\frac{t}{t^{,}}\,=\,\frac{4^{2}}{4^{2}-1{,}6^{2}}\,=\,\frac{16}{13{,}44}\,\dot=\,1{,}19\,.\]



